DataStructure-Tree

常见二叉树类型

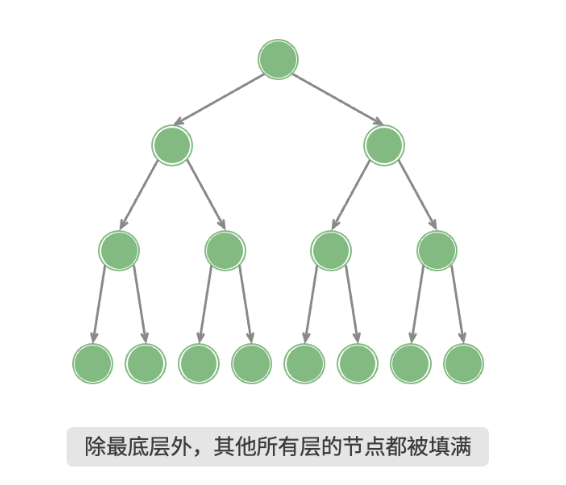
完美二叉树（满二叉树）

除了最底层外，其余所有层的节点都被完全填满。在完美二叉树中，叶节点的度都为0，其余所有节点的度都为2，如果树的高度为h，那么节点总数是2^h+1^ - 1。

如图

完美二叉树

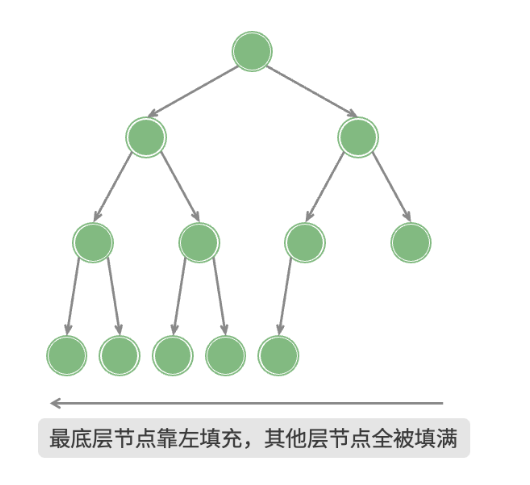
完全二叉树

只有底层没有被填满，且最底层节点尽量靠左填充。

完全二叉树

完满二叉树

除了叶子节点之外，其余所有节点都有两个子节点。

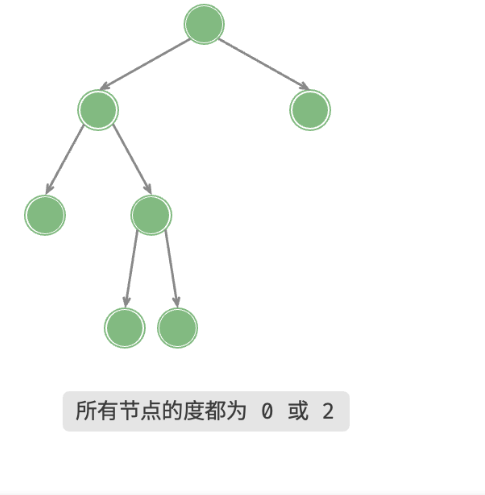
完美二叉树

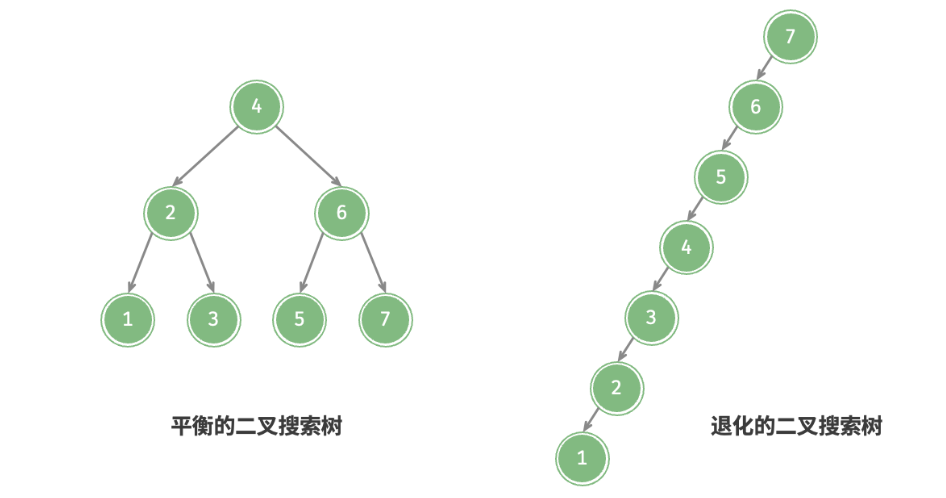
平衡二叉树

任意节点的左子树和右子树的高度之差绝对值不超过1

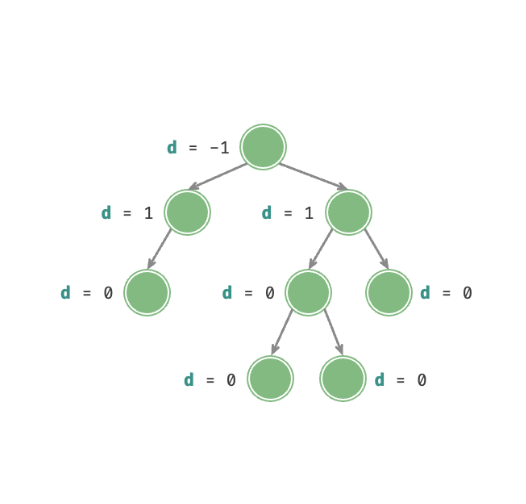
平衡二叉树

二叉树如果没有特殊限制（例如平衡二叉树）的话，可能会成为线性结构。即子节点要么全部在左子树，要么全部在右子树。

二叉树遍历

层序遍历（广度优先遍历）

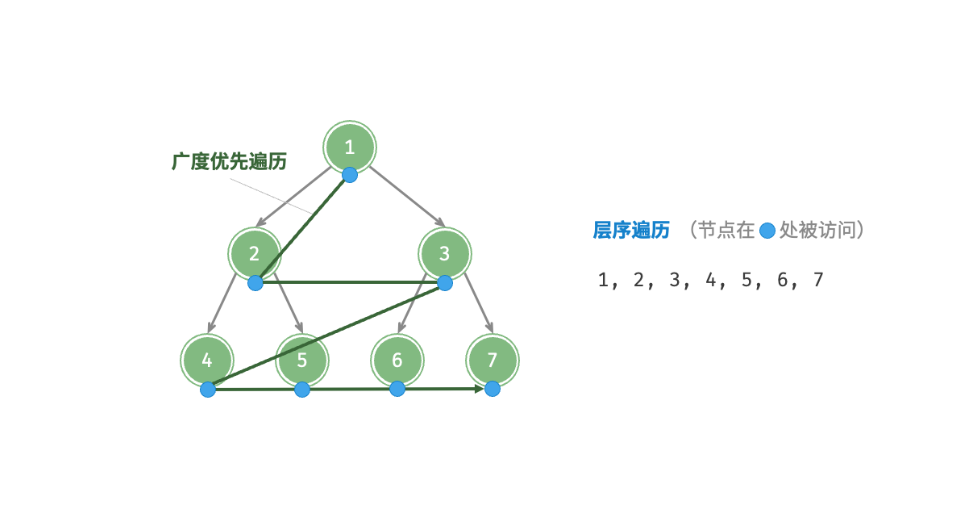
广度优先遍历

一般通过队列实现，队列遵循“先进先出”的规则，广度优先是“逐层推进”十分相似。

代码示例如下：

/* 层序遍历 */
List<Integer> levelOrder(TreeNode root) {
    // 初始化队列，加入根节点
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    // 初始化一个列表，用于保存遍历序列
    List<Integer> list = new ArrayList<>();
    while (!queue.isEmpty()) {
        TreeNode node = queue.poll(); // 队列出队
        list.add(node.val);           // 保存节点值
        if (node.left != null)
            queue.offer(node.left);   // 左子节点入队
        if (node.right != null)
            queue.offer(node.right);  // 右子节点入队
    }
    return list;
}

流程如下：

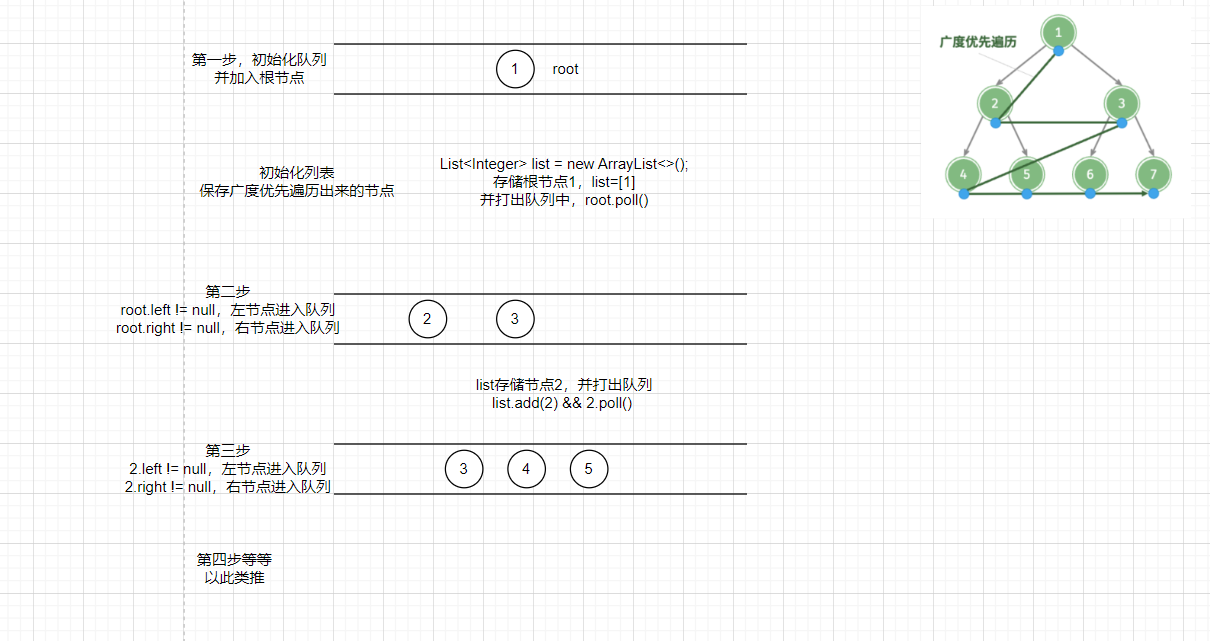
时间复杂度：所有节点被访问一次，使用 O(n) 时间，其中n为节点数量。

空间复杂度：在最差情况下，即满二叉树时，遍历到最底层之前，队列中最多同时存在 (n + 1) / 2个节点，占用 O(n) 空间。

前序、中序、后序遍历（深度优先遍历）

主要的思想就是“先走到尽头，再回溯继续”的遍历方式。

前序遍历：遵循根->左->右

中序遍历：遵循左->根->右

后序遍历可以看成高仿版的倒过来的层次遍历，只不过是对于左子树或者右子树来说，从叶子结点向上依次遍历遵循左->右->根。

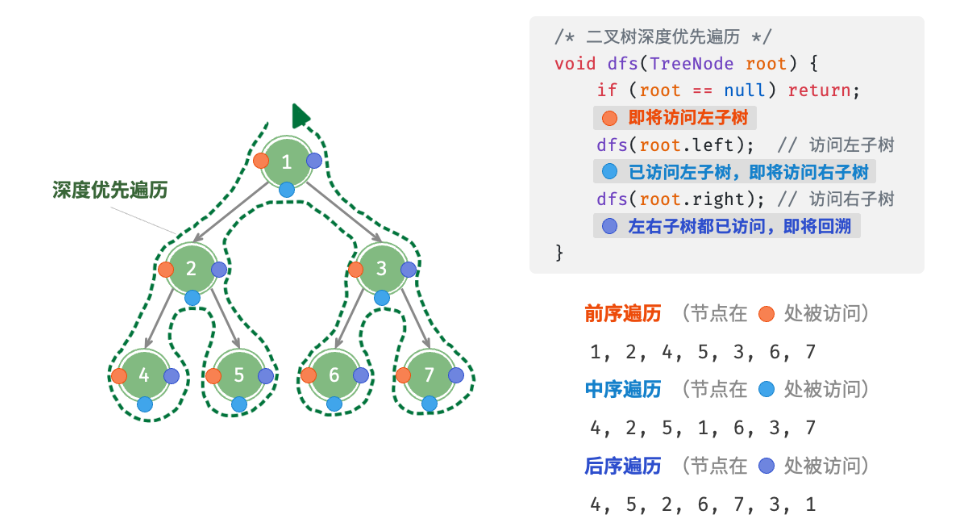
代码样例如下:

/* 前序遍历 */
void preOrder(TreeNode root) {
    if (root == null)
        return;
    // 访问优先级：根节点 -> 左子树 -> 右子树
    list.add(root.val);
    preOrder(root.left);
    preOrder(root.right);
}

/* 中序遍历 */
void inOrder(TreeNode root) {
    if (root == null)
        return;
    // 访问优先级：左子树 -> 根节点 -> 右子树
    inOrder(root.left);
    list.add(root.val);
    inOrder(root.right);
}

/* 后序遍历 */
void postOrder(TreeNode root) {
    if (root == null)
        return;
    // 访问优先级：左子树 -> 右子树 -> 根节点
    postOrder(root.left);
    postOrder(root.right);
    list.add(root.val);
}

时间复杂度：所有节点被访问一次，使用O(n)时间，其中n为节点数量。

空间复杂度：在最差情况下，即树退化为链表时，递归深度达到n，系统占用 O(n)栈帧空间。

上述代码实际上使用的就是递归的思想：

递：表示开启新方法，程序在此过程中访问下一个节点

归：表示函数返回，代表当前节点已经访问完毕

二叉树数组表示

表示完美二叉树

根据层序遍历的特性若节点的索引为i，则该节点的左子节点索引为2i + 1 ，右子节点索引为2i + 2

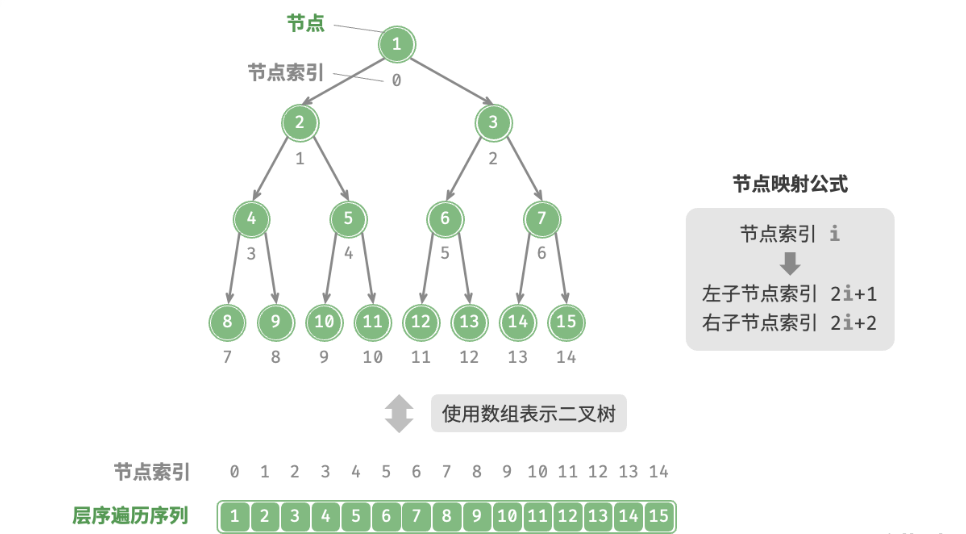
表示任意二叉树

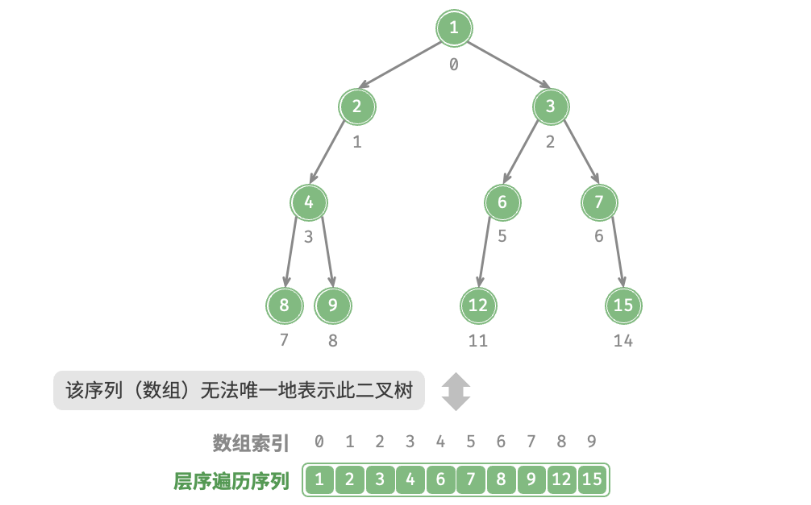
这个时候就不能通过公式的方式获取到对应的索引下标了，那么我们就可以通过层序遍历显式的写出所有NULL，对于上图代码如下。

1
2
3

/* 二叉树的数组表示 */
// 使用 int 的包装类 Integer ，就可以使用 null 来标记空位
Integer[] tree = { 1, 2, 3, 4, null, 6, 7, 8, 9, null, null, 12, null, null, 15 };

对于完全二叉树，由于它是只有最底层且靠右的位置才会出现无子节点的情况，所以所有的null都只会出现在数组的末尾，可以通过数组的方式来按顺序存储。

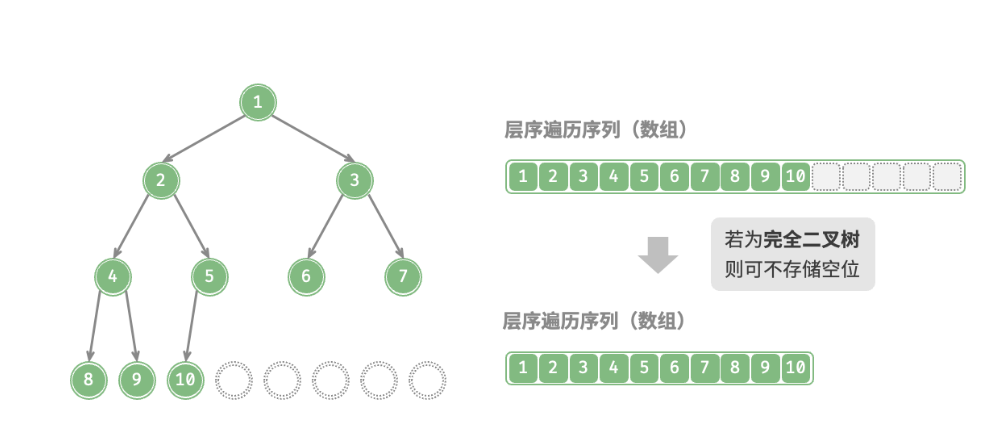
优势和弊端

优势：

数组存储在连续的内存空间中，对缓存友好，访问与遍历速度较快。
不需要存储指针，比较节省空间。
允许随机访问节点。

弊端：

数组存储需要连续内存空间，因此不适合存储数据量过大的树。
增删节点需要通过数组插入与删除操作实现，效率较低。
当二叉树中存在大量 NULL 时，数组中包含的节点数据比重较低，空间利用率较低。

二叉搜索树

满足条件（性质）：

左右子树所有节点值 < 根节点值 < 右子树所有节点的值

查找节点：

给出目标值num，需要在树中找到和num相等的节点。可以声明一个cur节点表示目前所指向的节点的位置。

如果cur.val < num，说明目标节点在cur的右子树中，执行cur = cur.right;
如果cur.val > num，说明目标节点在cur的左子树中，执行cur = cur.left;
如果cur.val = num，说明找到了目标节点，直接返回cur即可。

代码实现如下：

/* 查找节点 */
TreeNode search(int num) {
    TreeNode cur = root;
    // 循环查找，越过叶节点后跳出
    while (cur != null) {
        // 目标节点在 cur 的右子树中
        if (cur.val < num)
            cur = cur.right;
        // 目标节点在 cur 的左子树中
        else if (cur.val > num)
            cur = cur.left;
        // 找到目标节点，跳出循环
        else
            break;
    }
    // 返回目标节点
    return cur;
}

插入节点

给定一个待插入元素 num，根据二叉搜索树性质，思路如下：

1、查找出插入的位置，通过搜索的方式，从根节点出发，比较当前节点和num的大小，循环向下搜索直到越过叶子结点（遍历至null）时跳出循环。

2、初始化节点num，并将此节点置于null的位置。

注意：

二叉搜索树不允许存在重复节点，否则将违反其定义。因此，若待插入节点在树中已存在，则不执行插入，直接返回。

为了实现插入节点，我们需要借助节点 pre 保存上一轮循环的节点。这样在遍历至 NULL时，我们可以获取到其父节点，从而完成节点插入操作。

/* 插入节点 */
void insert(int num) {
    // 若树为空，直接提前返回
    if (root == null)
        return;
    TreeNode cur = root, pre = null;
    // 循环查找，越过叶节点后跳出
    while (cur != null) {
        // 找到重复节点，直接返回
        if (cur.val == num)
            return;
        pre = cur;
        // 插入位置在 cur 的右子树中
        if (cur.val < num)
            cur = cur.right;
        // 插入位置在 cur 的左子树中
        else
            cur = cur.left;
    }
    // 插入节点
    TreeNode node = new TreeNode(num);
    if (pre.val < num)
        pre.right = node;
    else
        pre.left = node;
}

与查找节点相同，插入节点使用 O(log n)时间。

删除节点

大概思路就是先查找到要删除的节点，然后进行删除，具体思路如下：

1、如果要删除的节点的度（子节点个数）为0的话，表示待删除的节点是叶子结点，可以直接删除

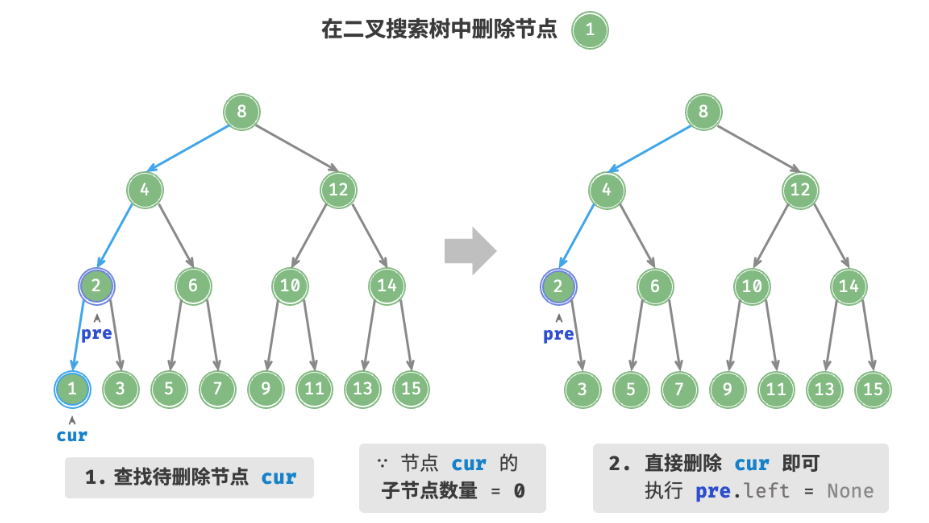
2、如果要删除的节点的度是1的话，就将待删除节点替换成其子节点即可。

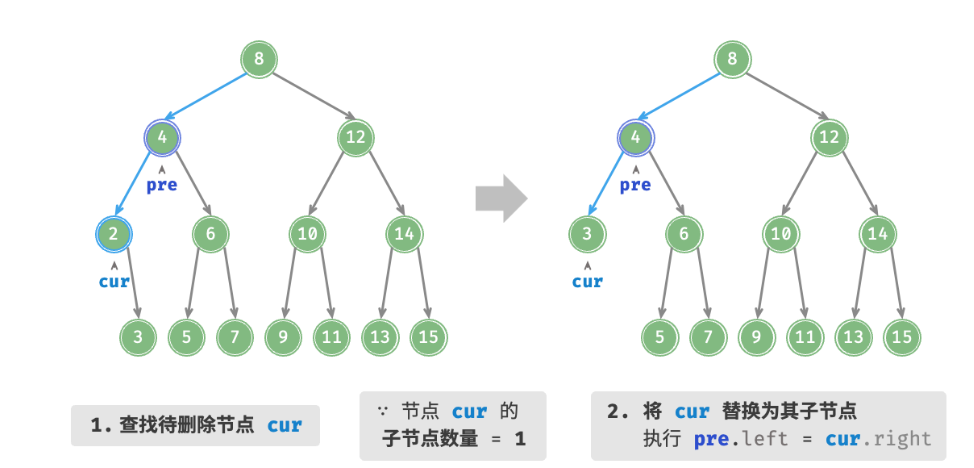
3、如果要删除的节点的度是2的话，所以可以用这个要删除的节点的右子树的最小节点或者左子树的最大节点进行替换。（保持二叉搜索树“左 < 右 < 根”的性质）

拿右子树的最大节点举例（即要删除的节点的中序遍历的下一个节点）：

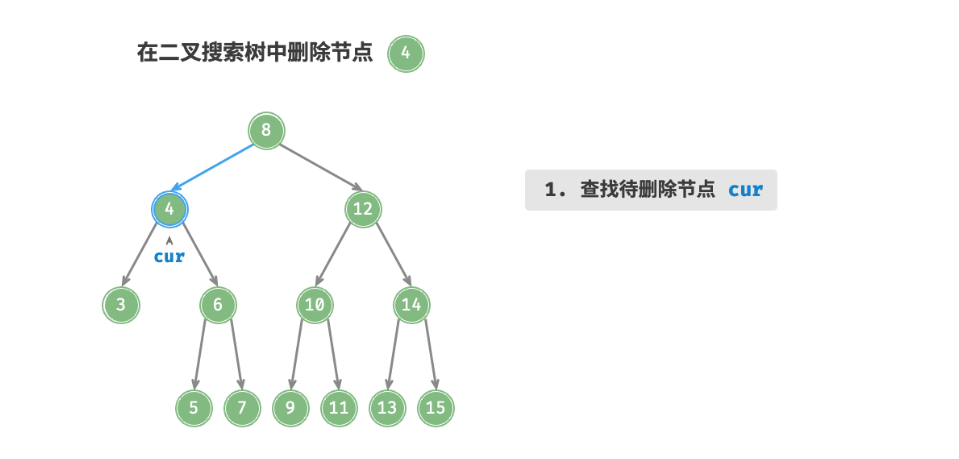
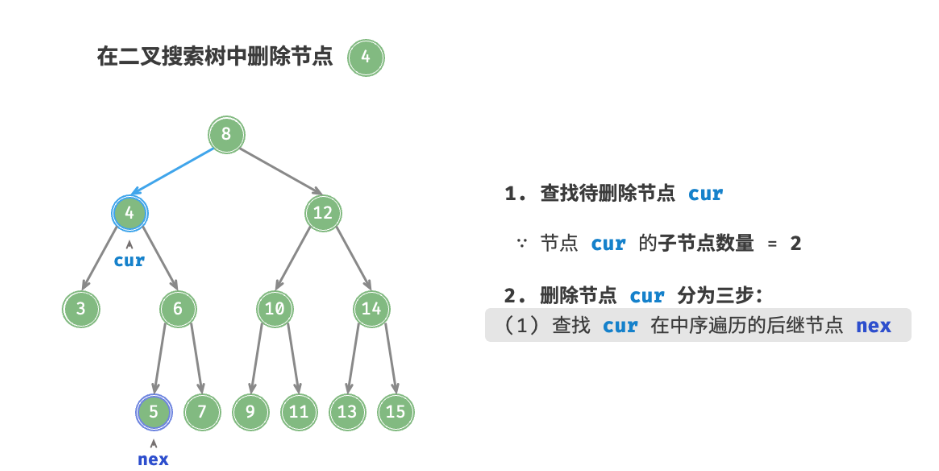
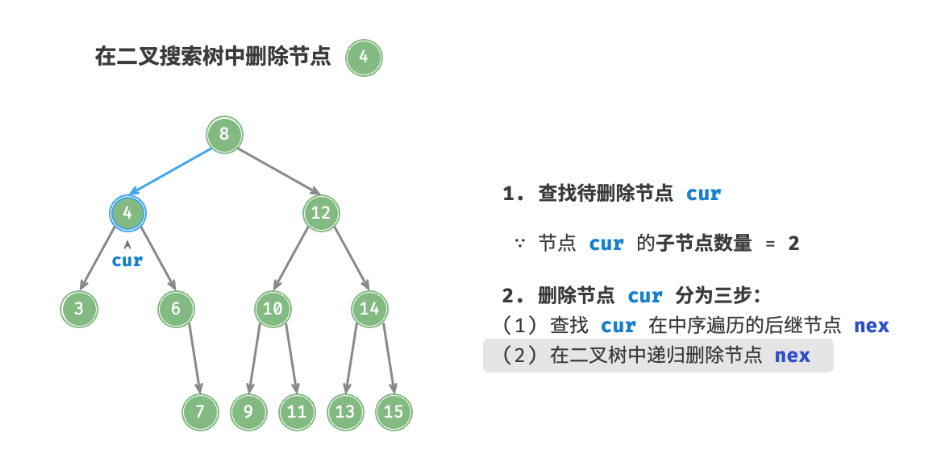
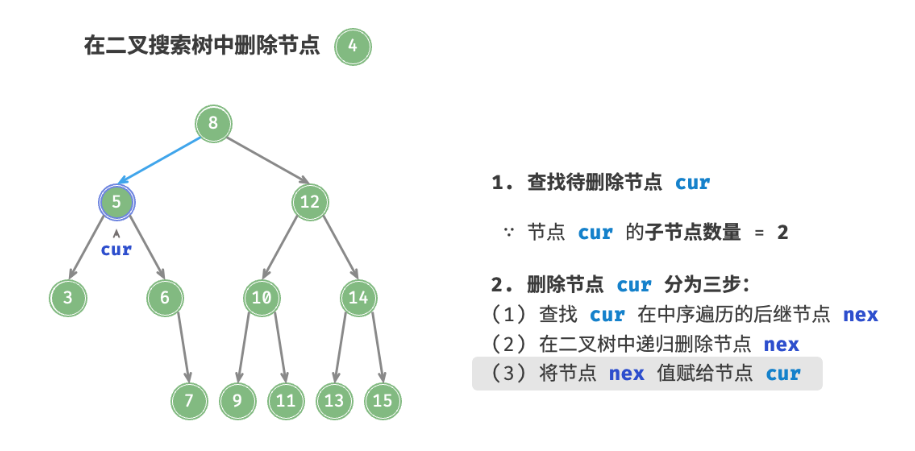
删除节点操作同样使用O(log n)时间，其中查找待删除节点需要 O(log n)时间，获取中序遍历后继节点需要 O(log n) 时间。

实现代码如下：

/* 删除节点 */
void remove(int num) {
    // 若树为空，直接提前返回
    if (root == null)
        return;
    TreeNode cur = root, pre = null;
    // 循环查找，越过叶节点后跳出
    while (cur != null) {
        // 找到待删除节点，跳出循环
        if (cur.val == num)
            break;
        pre = cur;
        // 待删除节点在 cur 的右子树中
        if (cur.val < num)
            cur = cur.right;
        // 待删除节点在 cur 的左子树中
        else
            cur = cur.left;
    }
    // 若无待删除节点，则直接返回
    if (cur == null)
        return;
    // 子节点数量 = 0 or 1
    if (cur.left == null || cur.right == null) {
        // 当子节点数量 = 0 / 1 时， child = null / 该子节点
        TreeNode child = cur.left != null ? cur.left : cur.right;
        // 删除节点 cur
        if (cur != root) {
            if (pre.left == cur)
                pre.left = child;
            else
                pre.right = child;
        } else {
            // 若删除节点为根节点，则重新指定根节点
            root = child;
        }
    }
    // 子节点数量 = 2
    else {
        // 获取中序遍历中 cur 的下一个节点
        TreeNode tmp = cur.right;
        while (tmp.left != null) {
            tmp = tmp.left;
        }
        // 递归删除节点 tmp
        remove(tmp.val);
        // 用 tmp 覆盖 cur
        cur.val = tmp.val;
    }
}